Introduction
Trempealeau County is located in
Western Wisconsin (Figure 1), being focus for
many sand mining companies to establish their business in. From the western
Wisconsin counties, Trempealeau has one of the more detailed and accurate
geodatabase, regarding not only the mines but many other features.
For that reason, this will be the
area of interest for this project, which intends to use raster advanced tools
to create a suitability model for sand mining – where the county areas will be
defined with different levels of being appropriate for this specific activity.
Considering the risks associated with sand mining, the same analysis will be
made regarding where the impact is higher or lower.
The analysis will be done by the
use of the Arc GIS software and it will have a modeling approach with the use
of Model Builder – in a way that the tools can be easily changed and adapted
for any future findings.
Figure 1 - Trempealeau County
Methodology
Suitability Analysis
The first section of this project
intends to study the distribution of geology units, land use, distance to the
rail depots, slope and water elevation to result in an index showing the best
locations to establish a sand mine. These criteria are related to the interests
of the owner and do not take in consideration the risk related to the sand
mining activity. This analysis will be done later on in the second section.
Digitizing the “Bedrock Geology
of Wisconsin, West-Central Sheet” map was necessary to have the precise
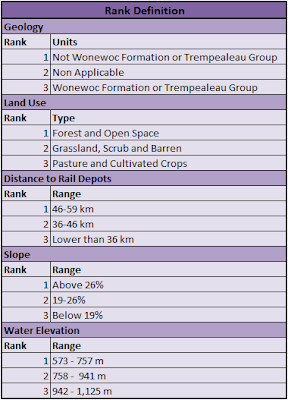
locations where Wonewoc Formation and Trempealeau Group were found (Figure 2). These geology units are the more appropriate
to extract frac sand, and therefore, represent high suitability (Rank 3 – Figure 3), while any other unit would have low
suitability (Rank 1 – Figure 3). Topology and
data integrity were guaranteed by establishing domains for the new feature
class and by using the cut tool during the digitizing session – as well as
validating new rules (Must Not Overlap and Must Not Have Gaps) and fixing any
errors found.
Figure 2 - Digitizing Process for Geology Units
Considering the land use found on
the National Land Cover Database 2006, the best locations are the ones where it
would be easier for the owner to establish a sand mine, like a Pasture and
Cultivated Crops (Rank 3 – Figure 3); where it
wouldn’t be necessary to remove any sort of vegetation like Grassland, Scrub or
Barren (Rank 2 – Figure 3) or dense types of
vegetation as forest (Rank 1 – Figure 3). Open
space was also considered for the index because is the only developed area with
no presence of dense population. However, other areas with low, medium or high
density were extremely not appropriate for sand mining, and therefore were
erased from the model.
Figure 3 - Rank Intervals for Suitability Criteria
Another important factor when
choosing the appropriate area to establish a sand mining is the transportation
cost. Because this resource is commonly transported by railroads, it’s better
for the owner to be close to the railroad terminals. Wisconsin rail depots were
available and were used to run Euclidean Distance in Trempealeau County – in
this matter, it’s important to remember that the real-world distance for this
case shouldn’t be Euclidean, but Manhattan distance. An approach with network
analysis as observed in previous exercises could be useful. Euclidean distance
will be used for simplicity purposes though. As it’s important to limit the
results only to the area of interest, a mask based on the county boundary would
result in a distorted result, since there are no depots inside it. To go around
this problem, a polygon was drawn within the closest depots and used as a mask.
Because the west extent of the county exceeds the west extent of the depots,
the result didn’t cover the entire county (Figure 4).
A fake depot was created far west from the county – to guarantee that it
wouldn’t affect the distance found by the tool – and then deleted after
acquiring the appropriate results (Figure 5). The
definition of ranks was based on how far the values were from the mean (41km),
the range of the first Standard Deviation (10 km) resulted on the medium rank, while the other ranks
were based in what was left from this interval, always thinking – the closer,
the better.
Figure 4 - Problems faced with Euclidean Distance
Figure 5 - Problem-Solving with Hypothetical Feature
A really steep area is also not
appropriate for sand mining, so the calculation of slope was necessary to find
the appropriate areas. For that, the DEM obtained by USGS was used to run the
slope tool. Because the result was too coarse, focal statistics were used to
smooth the slope values. The identification of which interval of slope was hard
to be found in the literature, so a different path was taken to determine that.
The Extract Values to Points tool (Figure 7) was
used to obtain the slope the existing mines are located in. By analyzing the
statistics, the most appropriate areas would be in the interval of the first
standard deviation (5.5% - 19.2%). Therefore, values lower than 19% obtained a
high rank. The interval between the first standard deviation and the second
standard deviation (19.2%-26%) resulted in the medium rank; while any
percentage slope higher than that would have the lower rank (Figure 6).
Figure 6 - Slope Intervals for Ranking
For last, the sand mines need to
have easy access to water because this resource is essential to separate the
different sizes of sand grains. Therefore, water table elevation contours were
obtained from the Wisconsin Geological Survey and then converted to a raster
with the Topo to Raster tool. Then, the values were categorized in three ranks
based on an equal interval classification – the closer to the surface, the
higher the elevation, the better for the sand mine owner.
Figure 7 - Suitability Model
After all the criteria were
categorized by the Reclassify tool, the Raster Calculator tool was used to obtain
the index, ranging from 1 (lowest suitability) to 15 (highest suitability). The
urban and wet lands needed to be removed, so after a binary reclassification
(wet and urban areas are 0 and others are 1), this raster was multiplied by the
previous, resulting in a more complete index for sand mining suitability.
Impact Index
As mentioned, the second section
will then study the impact of sand mining that can have three dimensions: the
soil fertility where it’s located, the noise and dust that can reach urban
areas, schools, rivers and airports, as well as the visibility from traditional
parks and trails located in Trempealeau County. All the features for this
section – with exception of the elevation model – were obtained by the official
Trempealeau County Geodatabase, available online.
It’s not appropriate that the
sand dust reach rivers, once that would change the environmental dynamic by the
accumulation of grains. In the same way, it should not be present in densely
populated areas, as schools and urban. For last, the dust could compromise
airplane pilot visibility essential to landing and takeoff. Considering the 640
meters range of the noise and dust shed, for all these features, the highest
risk would be in distances smaller than 640 meters, the medium would be between
that and its double – 1280 meters – and then, the lowest risk would be distances
higher than 1280 meters (Figure 8).
However,
when deciding which features to use to apply the euclidean distance, some
elements should be considered. There are a few ways to determine where are the
“densely populated areas”. Although the National Land Cover Database was
already downloaded, it was made for a larger area and it might be, then,
generalized. Because of that, the Zoning Districts feature class obtained
specifically from the county geodatabase was used. Also, for the streams, if
the entire feature class was considered, no areas in the county would have low
risk. Hence, it’s important to find which types would be more important, and
for that, the ones with Primary Flow in Water Perennial were selected and
exported as a new feature class, and this one was in fact used for the
Euclidean distance.
Figure 8 - Rank Intervals for Risk Criteria
Trempealeau County also has
important statewide trails and parks, and it wouldn’t be a good think that their
viewpoints would actually show a sand mine instead of a nice view. That would
compromise the tourism in the area, and therefore its economy. Therefore, the
application of the Viewshed Tool on the trails and parks – based on the USGS
elevation – would result in two distinct classifications over the entire
county: areas visible from the trails and parks, and areas not visible by them.
For last, a polygon feature class containing different types
of land allowed to find where the most fertile areas were. In other words,
areas where the sand mines shouldn’t be located at. The highest impact is in
prime farmland or farmland considered of statewide importance. Some areas were
prime land if some conditions were met, for instance, being drained and/or not
flooded during growing season. Because they are only prime farmlands if those
criteria are met, their risk level was considered medium. For last, areas that
were not prime farmland had a low risk rank. For last, the ranked raster were
added to each other using the Raster Calculator, resulting in a raster index
model, ranging from 1 - lowest impact - to 21 - highest impact (Figure 9).
Figure 9 - Risk Model
Results
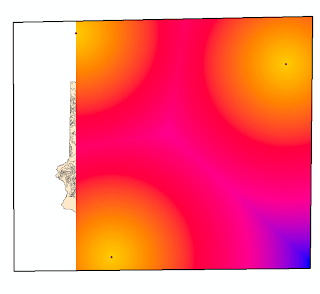
By the examination of the Figure 10, there are limited areas that are completely
not suitable due the land use – located mainly in the south – close to the main
river – as well in some areas close to the streams. Mainly, the predominance of
yellow colors in the map reveals an interval between 8 and 12 in the index,
which can be considered reasonable, considering the extension of these values
over the county. However, there is no doubt that the northern area has more
advantages when establishing a sand mine, where there are more locations with
the top level – 15.
Unfortunately, the suitability
model does not match that much with the risk model (Figure
11). In other words, there are limited areas with high suitability and
low risk at the same time. For the impact model, the county is almost
completely taken by the reddish colors referred to risk levels between 16 and
21 (the maximum). A few areas in the north are covered by greenish colors,
representing low risk; which fortunately can be overlapped by the same areas of
medium to high suitability in the previous model.
Figure 10 - Suitability Map
Figure 11 - Risk Analysis Map
Discussion
It’s interesting to notice the
contradiction between suitability and risk. The suitability brings the interest
of the companies that will establish their mines, in making it more profitable
and economically encouraging. It would be easier to decrease the social and
environmental risk not only for sand mining, but many industries establishments
if the variables for suitability locations matched to the low-risk areas.
However, as seen in the results, this is not trivial – in many cases, a low
risk area is not suitable or has low suitability for the activity being
proposed. Companies tend to be more driven by the economic outcomes rather than
the impact they will cause in the society and environment – unless regulations
require them to, being constantly enforced. The result is society and
environment being frequently impacted and a high demand for the government to
solve these issues – while it could have been prevented from the beginning, at
the establishment of the organizations.
Regarding the data and the
process, it’s important to recall that the criteria is hypothetical and should
not be applied directly to a real-world specific situation – such as
establishing an actual sand mine in Trempealeau County. In these cases, a
detailed study should be made, going more deep on the criteria and rank
intervals. The procedures in GIS, however, would remain the similar and they
are the most important goal of this exercise.
This project included a number of
challenges related to the use of raster. Compared to vector, this model tends
to have much larger files, due to the cell size: the higher the resolution, the
larger the file and the harder to use it on hardware with low performance. The
same is true for vector: the higher the resolution (number of nodes in a feature),
the more computer demand you’ll have. However, this problem is higher when
dealing with raster. One example is the use of the viewshed tool (Figure 12): for each pixel, the tool has to take the
elevation of all the pixels in between to determine the visibility. The result
is a very time-demanding tool. While the tool naturally takes a long time to
run, the amount of 3 hours and 26 minutes is not common, and occurred due to
some issue with the server.
Figure 12 - Viewshed Tool
Some strategies to improve
analysis efficiency can be applied, though. The resolution being used needs to
fit the purposes of the project: although high resolutions are commonly
desired, in this case they might not be the best option. If only a high
resolution raster is available, resampling techniques can be used to increase
the pixel size. Another strategy is to put the “Extract by Mask” tool always
before all the others, in order to avoid analysis in unnecessary pixels and
make sure the analysis is being made only in your area of interest.
Conclusion
Despite the challenges faced, the
project was successful in using all the necessary tools to come to a complete
result. The need of rethinking different techniques to go around the problems
found was essential to acquire problem-solving skills and actually learn how to
deal with GIS independently, especially with the use of the Arc GIS Help
Desktop.
Regarding the findings, the
spatial analysis offers an alternative to find areas with both high suitability
and low risk. It was mentioned how hard it’s for these two variables be found
together, but it’s even harder – if even possible – to find these cases without
the spatial analysis. A deeper analysis of each criterion can find special
areas where both variables are found, which can be used by the government to
encourage sand mines to be established in that area, supporting planning
initiatives.
Data Sources and References
MRLC. National Land Cover Database, 2006. Available on <http://www.mrlc.gov/nlcd06_leg.php> Access on April 21st.
TREMPEALEAU COUNTY. Trempealeau County Geodatabase. Available on <http://www.tremplocounty.com/landrecords/lrd_Data_Dictionary.htm> Access on April 21st.